ML M12: Clustering

Basic Clustering Problem

Clustering is a type of unsupervised learning algorithm which assigns instances to groups based on similarity. Given a set of instances $\mathbf{X}$, clustering uses a predefined distance function to measure (inverted) similarity, then partitions instances according to distance.

Clustering Methods

Single Linkage Clustering

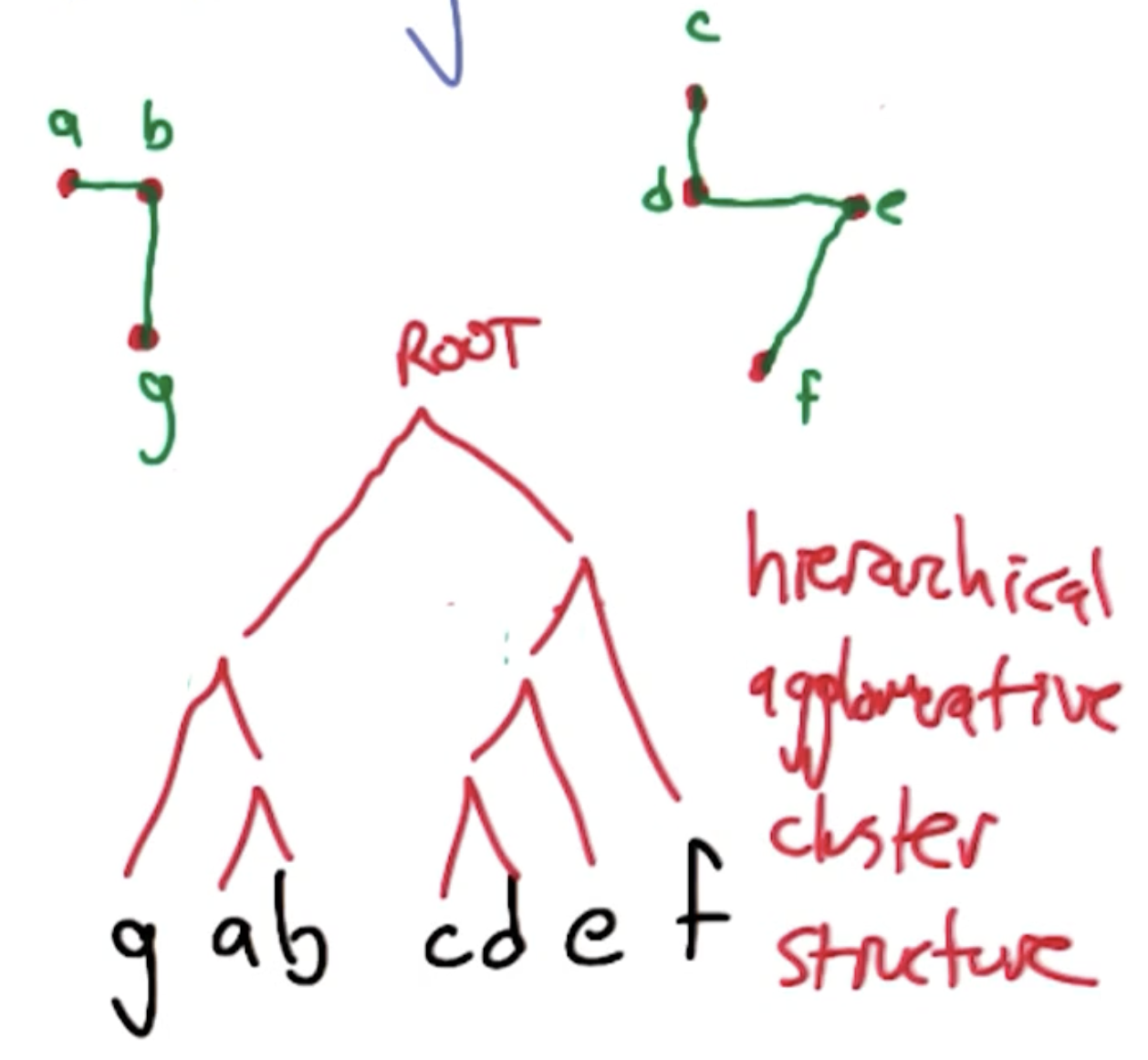
Single Linkage Clustering (SLC) is a hierarchical agglomerative clustering method, meaning we start with each instance as its own cluster and define groupings in a bottom-up fashion. SLC defines inter-cluster distance as the distance between the closest two points in the two clusters, and merges the two closest clusters at each iteration.

Repeat $n-k$ times to form $k$ clusters:

• Calculate inter-cluster distance between all clusters (using SLC method).
• Merge two closest clusters.

SLC is deterministic, meaning we will obtain the same result for any trial of SLC given the same data. Additionally, SLC has a time complexity of $O(n^3)$ in its most naive implementation.

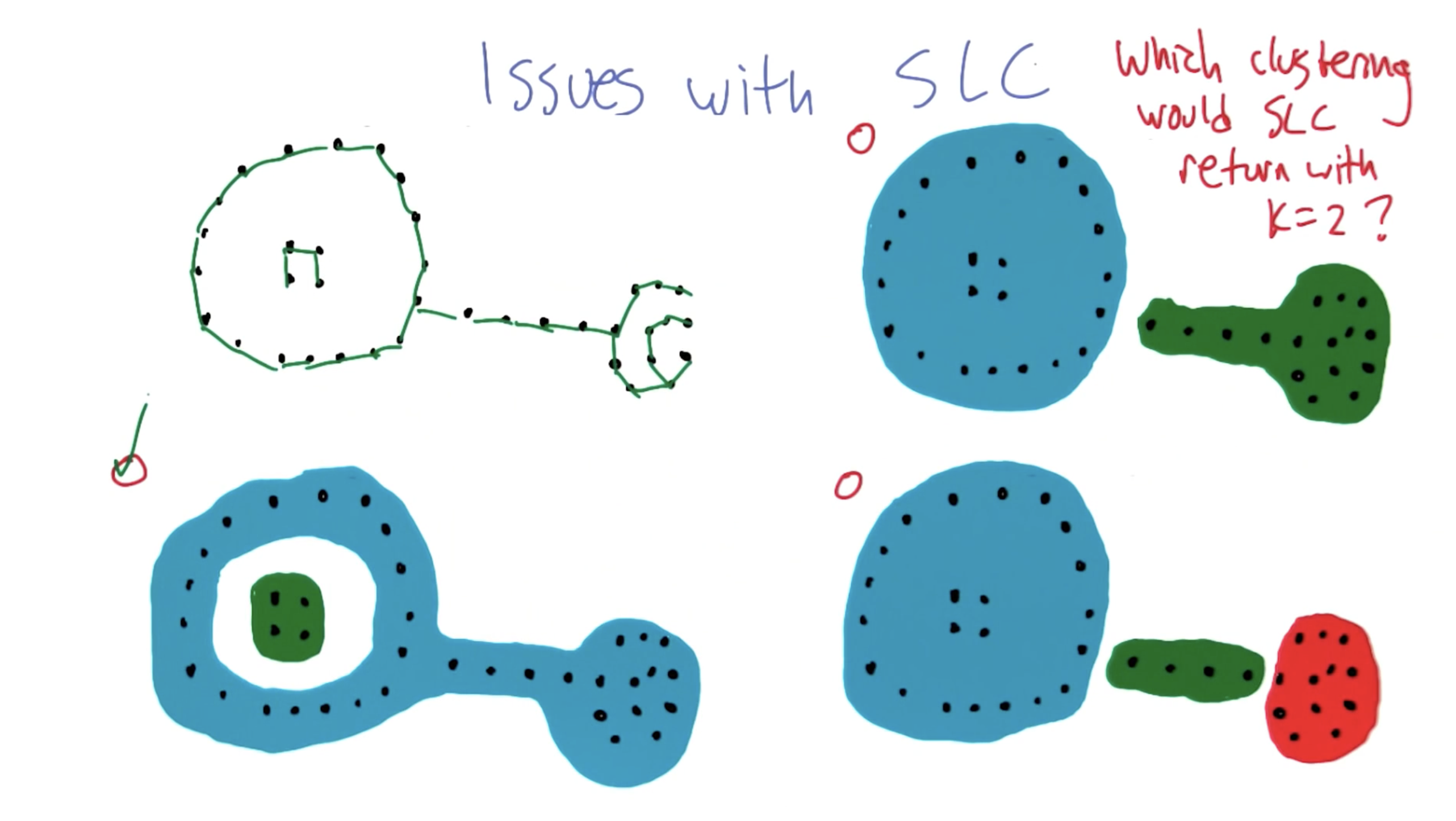
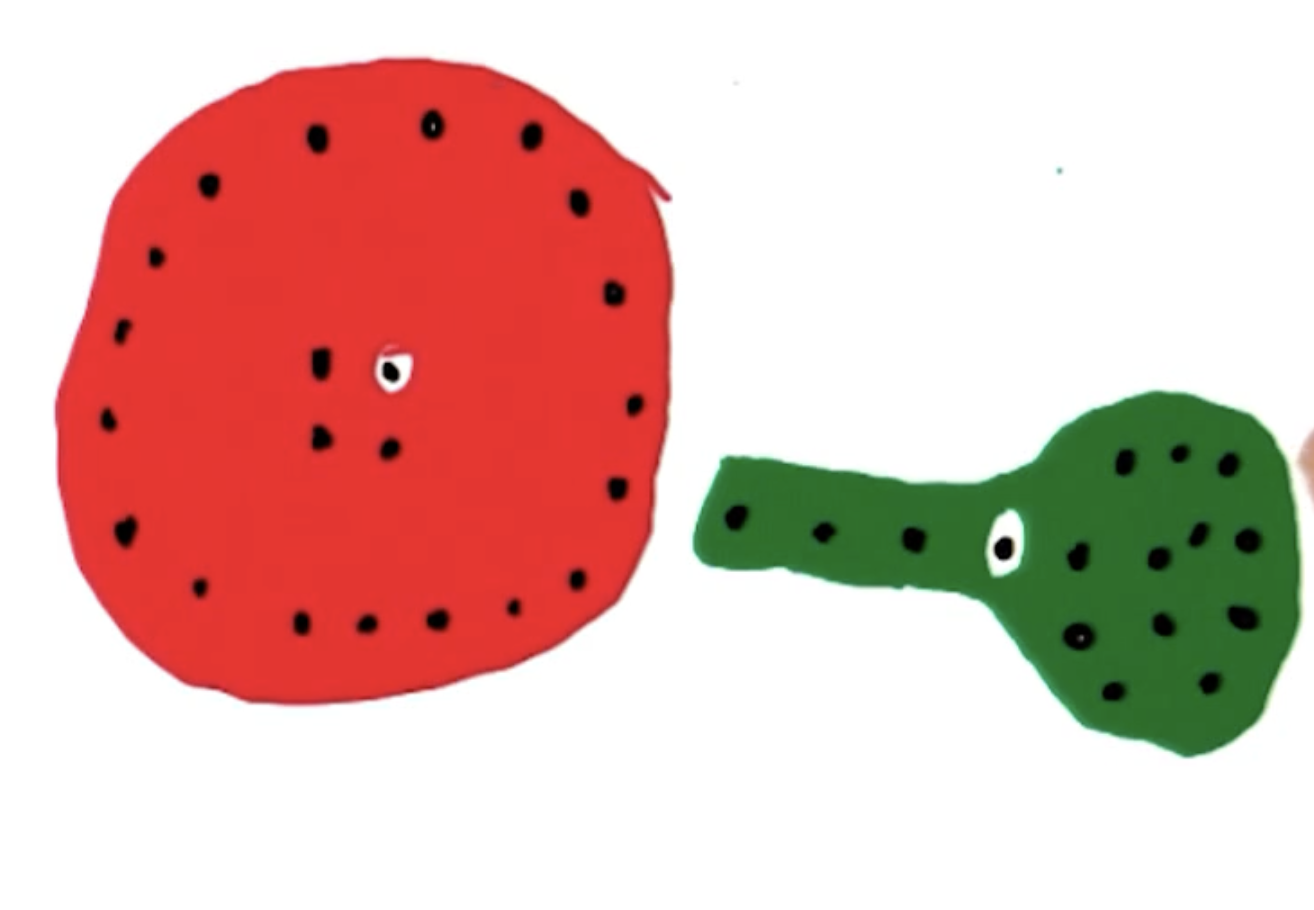
SLC is somewhat problematic in that it forms undesirable cluster shapes. This results from SLC defining inter-cluster similarity as the distance between any points across clusters, thereby causing a chaining effect.

K-Means

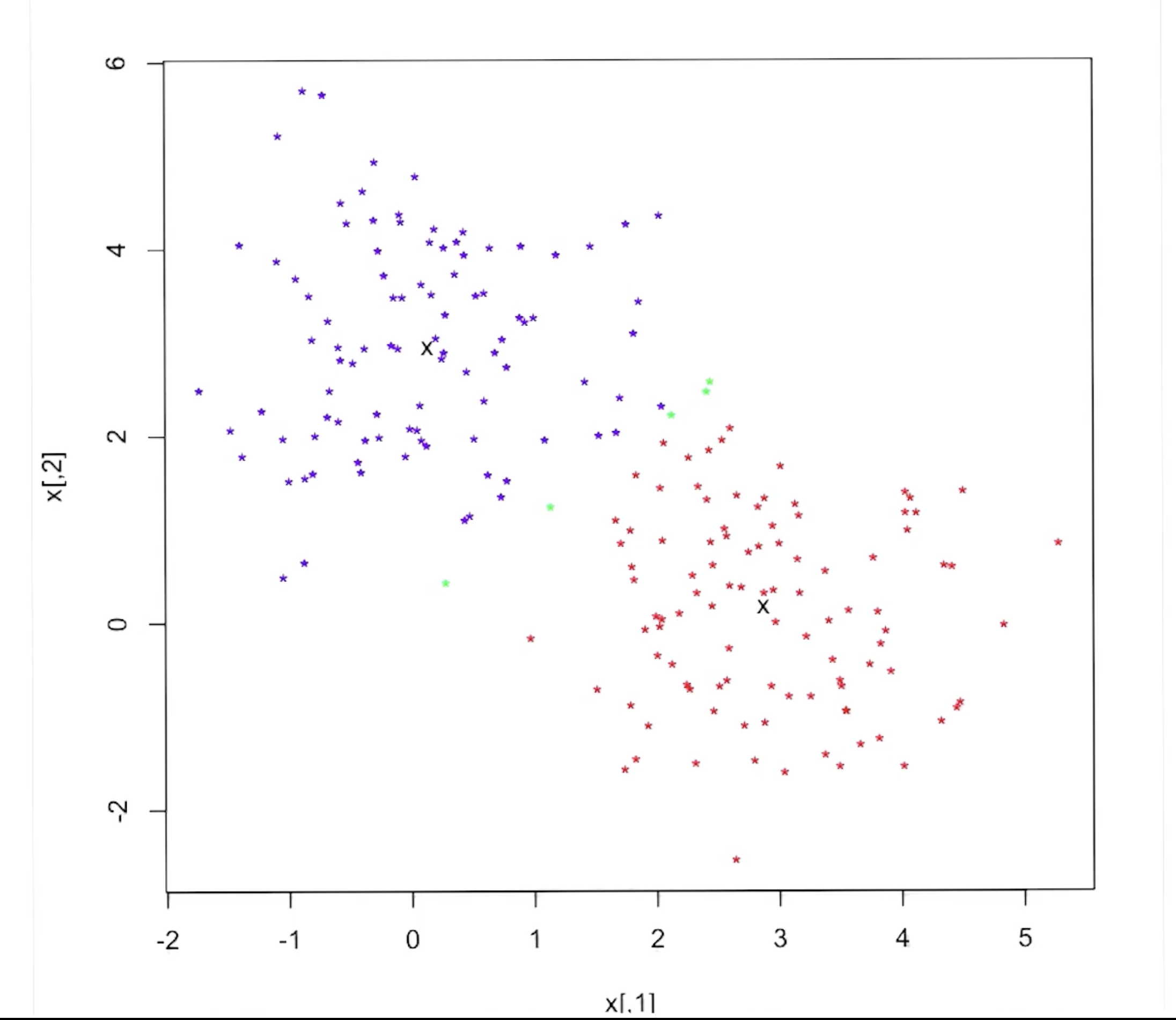
K-Means is an alternative clustering approach which defines clusters by calculating inter-object distance between each instance and each cluster centroid.

Initialize with $k$ cluster centroids (typically selected as random instances from dataset $\mathbf{X}$). Loop until cluster assignments converge:

• Compute inter-object distance between centroids and instances.
• Assign each instance to cluster with minimized distance.
• Re-compute cluster centroids by averaging over instances in the cluster.

\[\text{Assignment}: ~~ P^t(x) = \arg \min_i || x - \text{center}^t_i||^2\] \[\text{Centroid Calculation}: ~~ \text{center}^t_i = \frac{\sum_{y \in c^t_i} y}{|c_i|}\]

We can think of k-means as an optimization problem - we define our objective (error) function as the sum of distances between each instance and its cluster centroid.

K-means has the following properties:

• Each iteration is polynomial $O(k \times n)$.
• Guaranteed to converge in a finite number of steps $O(k^n)$.
• Can become stuck in local optima; random restarts are helpful here!

Expectation Maximization

To this point, we have only considered hard clustering algorithms, which assign instances to a single cluster in a binary fashion. Conversely, Soft Clustering methods probabilistically assign instances to clusters. This implies a single instance has a distribution over all possible clusters.

Expectation Maximization involves iterating between two calculations: expectation and likelihood maximization. During the expectation phase, we define soft cluster assignments; for likelihood maximization, we compute the new statistical parameters for each cluster distribution. Techniques such as Gaussian Mixture Modeling assume each cluster distribution is Gaussian, implying we estimate mean and variance.

\[\text{Expectation}: ~~ E[Z_{i, j}] = \frac{\Pr(X = x_i | \mu = \mu_j)}{\sum_j \Pr(X = x_i | \mu = \mu_j)}\] \[\text{Maximization}: ~~ \mu_j = \frac{\sum_i E[Z_{i, j}]x_i}{\sum_i E[Z_{i, j}]}\]

Expectation Maximization is convenient in that it does not force cluster assignment on particularly confusing instances. Additionally, it has the following properties:

• Monotonically non-decreasing likelihood.
• Not guaranteed to converge to the global optimum; can get stuck in local optima (unfortunately).
• Works with any distribution (as opposed to Gaussian).

Properties of Clustering

Ideal clustering algorithms have the following properties:

• Richness: for any assignment of instances to clusters, there is some distance matrix $D$ such that the clustering scheme returns desired assignments.
• Scale-Invariance: scaling distances by a positive value does not change clustering assignments.
• Consistency: decreasing intra-cluster distance and expanding inter-cluster distance does not change clustering assignments.

Unfortunately, no clustering scheme can achieve all three of these properties! This is known as the Impossibility Theorem.

---

(all images obtained from Georgia Tech ML course materials)